
Top > 無料統計ソフトRで心理学 > 雑多な知識: 7. Rによるシミュレーション
無料統計ソフトRで心理学
雑多な知識: 7. Rによるシミュレーション
目的
Rで「Simulationをすることで,ユーザーでも統計学の理解が深まる」事例を示します。
例題
- 臨床心理学では,しばしば,連続変数を中央値やcutoff pointで離散化するケースが見られます。
- たとえば,ベック抑うつ尺度(BDI)で「10点以上の被検者を抑うつ者」,「10点未満の被検者を非抑うつ者」と分離するケースです。 また,ツァン抑うつ性尺度(SDS)で,「中央値以上の被検者を抑うつ高群」,「中央値未満の者を抑うつ低群」と分離するケースも多く見られます。
- MacCallum et al. (2002) では,このような「恣意的な2値化」を行う問題点を,ユーザー向けに指摘しています。この文献で示されている,Simulationを一部,Rを用いて再現してみます。
引用文献: MacCallum, R. C., Zhang, S., Preacher, K. J., & Rucker, D. D. (2002). On the practice of dichotomization of quantitative variables. Psychological Methods, 7, 19-40.
手続き
- 母相関係数を決める (r=.1, .3, .5, .7, 9)。
- 2変量正規分布に従う母集団から,標本抽出する。標本サイズは,以下の通り (n=50, 100, 150, 200, 250, 300)。
- 積率相関係数を算出する。
- 片方の変数を中央値で分離する.その後,point-biserial correlationを算出する。
- point-biserial correlation が,積率相関係数よりも大きくなるか否か評価する。
- 10000万回,2-5の手順を繰り返す。
- point-biserial correlation が,積率相関係数よりも大きくなった数を数える。
Rプログラム
Step1: 特定の相関係数を持つ二変量データの生成(青木先生のプログラム)
| gendat2 <- function(nc, r) { # 仮のデータ行列を作る。この時点では変数間の相関は近似的に0である。 z <- matrix(rnorm(2*nc), ncol=2) # 主成分分析を行い,主成分得点を求める。この時点で変数間の相関は完全に0である。 res <- eigen(r2 <- cor(z)) coeff <- solve(r2) %*% (sqrt(matrix(res$values, 2, 2, byrow=TRUE))*res$vectors) z <- t((t(z)-apply(z, 2, mean))/sqrt(apply(z, 2, var)*(nc-1)/nc)) %*% coeff # コレスキー分解の結果をもとに,指定された相関係数行列 を持つように主成分得点を変換する。 z %*% chol(matrix(c(1, r, r, 1), ncol=2)) } |
Step2: 母集団を定義
| N <- 100000 rho <- .1 Rho <- gendat2(N,rho) |
#便宜的に,母集団の大きさを「100000」とする |
Step3: 標本抽出
n <- 50 |
#便宜的に,標本サイズを50とする #100000から50個,無作為に番号を選ぶ #母集団から,無作為に選んだ番号を指定して,標本抽出する |
Step4: 変数名を定義
x <- xd <- temp[,1] xd[x < median(x)] <- 0 |
標本抽出した1列目のデータを,x, xdと命名する |
Step5: 相関係数の算出
pearson <- cor(x, y) |
積率相関係数を算出する |
Step6: 反復計算
sim1 <- function(N, n, rho, iter){ for(i in 1:iter){ x <- xd <- temp[,1] xd[x < median(x)] <- 0 pearson <- cor(x, y) if(pb > pearson){ |
N=母集団の大きさ,n=標本サイズ,rho=母集団相関係数,iter=反復回数を引数とする関数を作成する. |
Step7: 小さな事例の確認
sim1(N=100000,n=50,rho=.1,iter=10000) |
母集団の大きさ=100000, 標本サイズ=50,母集団相関係数=.1, 反復回数= 10000の場合に, |
Step8: 論文の事例の確認
tab1 <- matrix(0,ncol=6, nrow=5) for(i in 1:length(Rho)){ |
5行6列の行列を作成 反復計算 |
結果の解釈
tab1のオブジェクトには,以下の表のようなデータが保存されています (無作為抽出の過程が入るので,追計算では全く同じ値にはならない)。
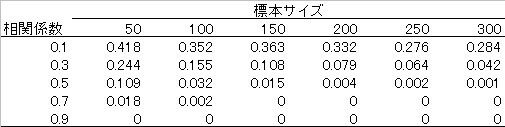
このデータから,以下の2点が考えられます (主に,sampling errorを示したいのだが)。
- 標本サイズと母集団相関係数が小さい場合,2値化することで相関係数を過大評価する (sampling error)
- 標本サイズと母集団相関係数が小さくない場合,2値化することで相関係数を過小評価する
したがって,臨床心理学などの,母集団相関係数が小さいことが多い領域での 2値化して得られた有意差は,sampling errorの可能性が高い。 また,2値化して有意差が得られなかった場合は,単に,検出力が低いことが原因かもしれない。2値化により,検出力と分散説明率が大幅に下がることは証明されているので,注意が必要です (詳しくは,MacCallum et al., 2002を参照下さい)。そもそも,わざわざ連続変数を離散化する理由が希薄なのです。
目次: 雑多な知識
Rの導入に関するポイントを書いています。
|
||
| Tweet |
|
著者: 奥村泰之 (Curriculum Vitae) |